Custódia de cripto descentralizada por limiar / threshold – Waves.Exchange
Este artigo traz uma revisão das soluções de custódia de cripto existentes, além de encontrar problemas comuns e propor uma nova abordagem descentralizada, identificando as armadilhas dos sistemas existentes.
O que é custódia de cripto e por que precisamos disso?
Gerenciar chaves secretas não é fácil. Eles são difíceis de lembrar e fáceis de perder. Podem ser roubadas, hackeadas ou reveladas acidentalmente a outras pessoas. A perda de uma chave secreta leva à perda total do acesso à conta do usuário e a todos os fundos associados a ela. O roubo de uma chave possibilita que o invasor roube os fundos ou faça operações não autorizadas, fingindo ser o proprietário da conta.
Todos esses riscos e restrições dificultam a interação de novos usuários com blockchains e outros sistemas criptográficos de chave secreta. Isso também dificulta que sistemas financeiros existentes, dependentes principalmente das técnicas de autenticação tradicionais, se integrem aos sistemas de chave secreta. Em resumo, a gestão de chaves secretas envolve riscos significativos em relação a perda ou roubo.
Para resolver esses problemas, foram propostas muitas soluções para custódia de cripto. Um custodiante é um sistema que oferece armazenamento seguro de chaves secretas de usuários, abstraindo a criptografia e a complexidade técnica dos sistemas de chave secreta subjacentes, enquanto fornece autenticação tradicional, como e-mail, senha ou telefone.
Problemas da Custódia Centralizada
A maioria dos custodiantes disponíveis no mercado são centralizados. Isso significa que há servidores verificando a identidade dos usuários, com bancos de dados que mantêm segredos completos do usuário (possivelmente em várias cópias, como backups), além de servidores usando segredos completos para gerar assinaturas digitais e interação de rede entre os componentes. Tudo isso pertencente a uma única pessoa ou organização.
A arquitetura centralizada tem vulnerabilidades inerentes. Um banco de dados com chaves secretas pode ser perdido ou roubado. Um servidor que gera assinaturas pode ser hackeado e vazar chaves secretas usadas no processo de assinatura. O spyware pode ser inserido para monitorar o tráfego da rede.
E o fator humano também não deve ser descartado. É comum que invasores explorem erros humanos para obter seus benefícios. Em qualquer sistema centralizado existem pessoas, administradores de sistema, equipe técnica etc, com acesso a subsistemas importantes. E mesmo uma única pessoa pode comprometer todo o sistema.
Custódia Descentralizada
Os problemas descritos acima têm a mesma origem: centralização. Uma única pessoa, um único servidor, um único banco de dados – se algum deles falhar, todo o sistema falhará.
Logo, como é possível evitar qualquer ponto de falha? Tornando o sistema descentralizado.
Inicialmente, vamos formular alguns requisitos para o sistema “ideal”:
1. Nenhuma pessoa deve ser capaz de comprometer o sistema.
2. Não deve existir nenhum armazenamento contendo chaves secretas completas.
3. Uma chave secreta completa nunca deve aparecer em um único servidor ou dispositivo.
A única maneira de satisfazer os requisitos acima é dividir uma chave em várias partes. Cada parte deve ser mantida separadamente, em bancos de dados e servidores mantidos por pessoas diferentes. Para executar as operações, os participantes precisam cooperar de alguma forma, sem nunca revelar suas partes secretas a ninguém.
Uma abordagem ingênua seria dividir a chave em n partes e exigir que todos os n participantes executem uma operação. No entanto, isso significa que um único participante comprometido ou offline compromete todo o sistema, o que quebra o requisito 1 e nos leva de volta ao ponto único de falha.
Portanto, o número de participantes cooperantes necessários para executar uma operação em nome do usuário deve ser menor que n. Considere t o número de participantes necessários para executar uma operação.
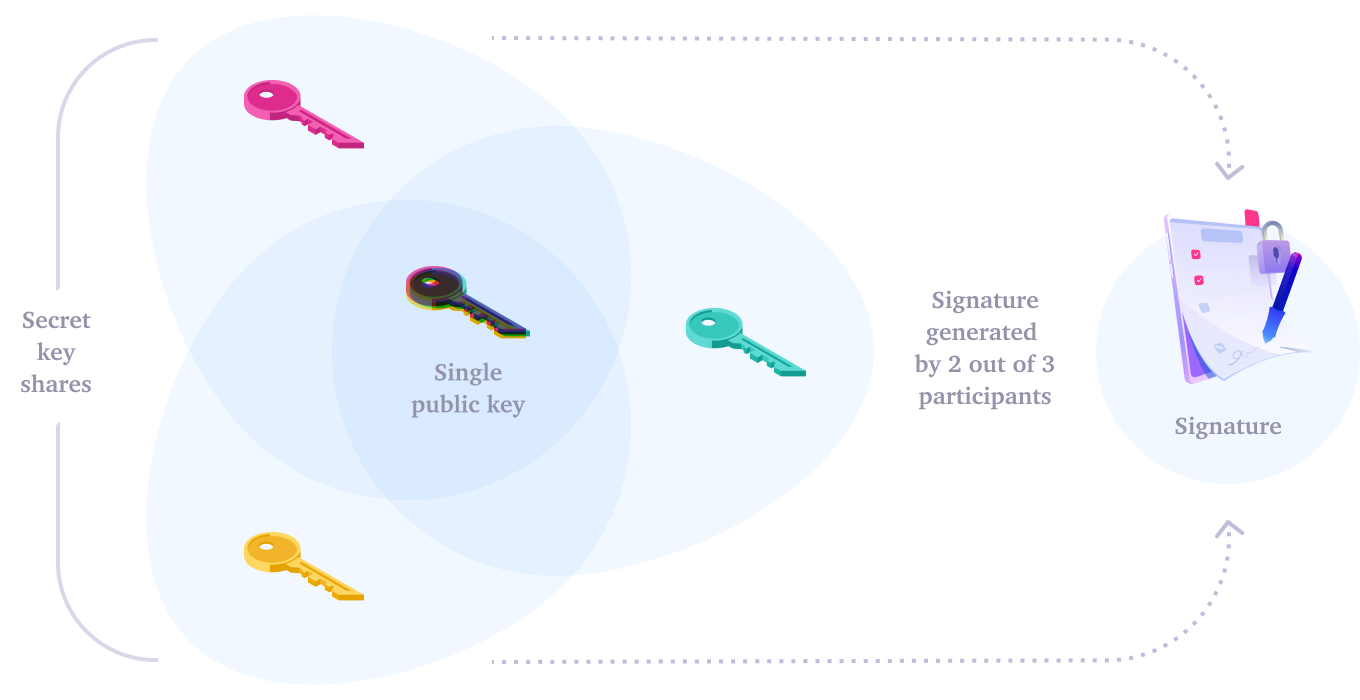
Esta solução apresenta vantagens em segurança e disponibilidade. Mas pelo menos t participantes precisam ficar comprometidos simultaneamente para comprometer todo o sistema. E o sistema ficará offline apenas se (n-t + 1) participantes ficarem offline ao mesmo tempo.
As ideias acima são inspiradas por abordagens conhecidas de segurança e criptografia, como o esquema Shamir Secret Share, autenticação multifator, assinaturas múltiplas e criptografia de limite.
Criptografia de Limiar
Para que um sistema funcione enquanto atende aos requisitos declarados acima, deve existir uma maneira para os participantes criarem assinaturas digitais em nome de usuários, sem nunca revelar sua parte da chave secreta ou recriar um segredo completo em uma única máquina.
Existe toda uma área de criptografia, dedicada apenas a isso: criptografia de limiar (threshold cryptography). Diversos algoritmos foram propostos para muitos esquemas de assinatura digital populares: RSA, ECDSA, EdDSA etc. A implementação desses algoritmos pode permitir que um custodiante opere entre blockchains diferentes, funcionando em muitos sistemas: Waves, Bitcoin, Ethereum ou outros.
Por enquanto, vamos nos concentrar no esquema de assinatura usado no blockchain Waves, baseado em EdDSA com Curve25519. Todos os valores escalares abaixo serão considerados em um subgrupo de ordem principal.
Assinatura com criptografia de limiar (t, n)
n – número de participantes
t – valor de limiar
q – sequência de subgrupo principal
B – ponto base da curva
A – chave pública do usuário
M – mensagem para assinar
si – parte da chave secreta do enésimo participante
Qualquer t de n participantes pode gerar uma assinatura. Para uma descrição simplificada, vamos assumir que a assinatura é gerada pelo participante Pi, i=1,…., t.
1. Pi gera um valor inteiro ri = SHA512 (const_prefix ║ si ║ M ║ random_64_bytes) mod q
2. Pi calcula e publica um ponto Ri= ri * B
3. Após cada Pi, publicar Ri, é calculado um ponto:
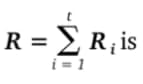
4. É calculado o valor k= SHA512 (R║A║M) mod q
5. É calculado o polinômio de Lagrange com coeficente zero:
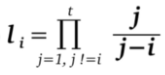
6. Pi calcula e publica Si = ri + k *li *si
7. É calculado o valor S:
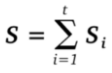
A concatenação dos valores (R,S) fornece a assinatura resultante.
Para verificar a assinatura, o verificador garante que 8 * S * B = 8 * R + 8 * K * A
Geração de chave descentralizada
De acordo com os requisitos 1 e 3, uma chave completa nunca deve aparecer em uma única máquina. Isso inclui a fase de criação do usuário e geração da chave. Portanto, é necessário um algoritmo que permita aos participantes cooperantes gerar partes de chaves secretas e a chave pública correspondente, sem revelar suas partes ou reunir uma chave completa em um só lugar.
Vários esquemas foram propostos para fazer isso. Baseamos nossa solução em um esquema proposto por Rosario Gennaro, Stanislaw Jarecki, Hugo Krawczyk e Tal Rabin em 1999.
Geração de chave descentralizada
n – número de participantes
t – valor de limiar (threshold value)
B – ponto base da curva
G – gerador, comum entre os participantes, “discreet logarithm” de G base B é desconhecido
Pi – enésimo participante
1. Pi gera um escalar secreto Xi e calcula Ai = Xi * B
2. Pi gera um escalar secreto ri e usa isso para calcular e publicar commit Ci = Ai+ ri * G
3. Quando todos os n participantes tiverem publicados seus ‘commits’, cada Pi publica Ri, abrindo assim Ci e permitindo que os outros participantes recuperem todo Ai
4. Uma chave pública resultante é calculada:
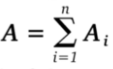
5. Pigera um polinômio aleatório com grau de no máximo t – 1 de modo que:
![]()
6. Pi calcula Fij = fij * B e transmite Fij para j = 1, …, (t – 1)
7. Quando todos tiverem enviado seus Fij, Pi envia secretamente sij = fi (j) e uma assinatura em sij para Pj para j = 1,….., n. Em especial, Pi mantém sii.
8. Pi verifica que a parte recebida de Pj é consistente com o valor publicado anteriormente ao verificar que:
![]()
Diversas estratégias foram propostas caso a da verificação acima falhe. Uma abordagem simples é a tentar novamente desde o início. Ou, em uma abordagem mais sofisticada, o participante pode publicar uma reivindicação, e se um número suficiente de reinvindicações for alcançado, o participante-remetente é marcado como não confiável e excluído.
9. Picalcula o resultado de sua parte da chave secreta:
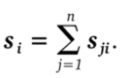
Redistribuição de partes da chave secreta
Um sistema de criptografia como o que estamos propondo deve considerar a segurança e a confiabilidade, não apenas em um ponto fixo no tempo, mas também por longos períodos. Para permitir isso, a rede não deve ser estática, mas flexível e adaptável às novas circunstâncias.
Nossa maneira de alcançar essa flexibilidade é por meio da redistribuição secreta das partes. Usando as partes existentes e várias rodadas de comunicação, t entre n participantes criam e distribuem novos conjuntos de partes a todos os participantes da rede atualizada, sem revelar nenhuma parte ou segredo completo. Após a conclusão, todos os participantes incluídos na redistribuição terão novas partes da chave secreta, incompatíveis com as antigas, mas as chaves públicas de todos os usuários permanecerão as mesmas.
Dado que tanto o número de participantes quanto o valor limite podem ser alterados, essa abordagem é genérica o suficiente para cobrir casos de uso como:
Caso de uso: participante perde dados
Solução: redistribuir partes “no local”: mesmos participantes, mesmo limite. Será criado um novo conjunto de partes para cada participante, inclusive aquele que perdeu os dados.
Caso de uso: participante revela dados
Solução: mesma solução: redistribuir “no local”. O participante recebe novas partes e as que foram reveladas se tornam inúteis.
Caso de uso: participante se torna desonesto
Solução: ‘Expulsar’ o participante da rede: redistribuir de uma forma que não inclua o participante em uma rede atualizada.
Caso de uso: participante sai
Solução: mesma solução.
Caso de uso: Novos participantes precisam ser adicionados
Solução: Redistribuir, envolvendo os novos participantes.
Caso de uso: alterações de valor limite
Solução: Redistribuir, definindo um novo limite de destino no algoritmo.
Um algoritmo baseado em um artigo de 1997, de Yvo Desmedt e Sushil Jajodia é proposto para nosso sistema, com verificações adicionais para maior segurança.
Redistribuição de partes do segredo
n – número de participantes antes da redistribuição
n’ – número de participantes após a redistribuição
t – valor de limiar antes da redistribuição
t’ – valor de limiar após a redistribuição
Pi – enésimo participante antes da redistribuição
Pi’ – enésimo participante após a redistribuição
si – enésima parte do segredo antes da redistribuição
si’ – enésima parte do segredo após a redistribuição
B – ponto base da curva
Qualquer t de n participantes pode iniciar a redistribuição. Para mantermos uma descrição simples, vamos considerar que a redistribuição é iniciada pelos participantes Pi = i =1, …, t.
1. Pi gera um polinômio aleatório com grau de no máximo t’ – 1 de modo que :
![]()
2. Pi calcula:
![]()
Em particular:
![]()
Todos os resultados Fij são transmitidos.
3. Quando todos tiverem enviado seus Fij, Pi envia sij= fi (j) secretamente e uma assinatura em sij para P’j, para j=1,….., n’.
4. P’jverifica que a parte recebida de Pi é consistente com o valor publicado anteriormente ao verificar que:
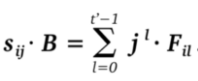
As verificações de consistência são iguais às do esquema de geração distribuída de chaves.
5. É calculado o coeficiente do polinômio de Lagrange em zero:
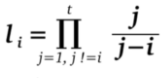
6. P’j calcula sua parte atualizada do segredo:
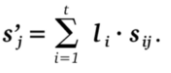
Após a reconstrução, os escalares resultantes s’j, j=1,….., n’ são os novas partes do segredo. A nova rede tem n’ participantes com limiar t’. Chaves públicas não são mudadas.
Autenticação do usuário
Até agora nos concentramos no aspecto criptográfico, ou seja, como a rede executa as operações. No entanto, para decidir se vai executá-las ou não, é necessário uma prova da identidade do usuário. Além disso, cada participante deve validar a identidade do usuário de forma independente e prosseguir para executar uma operação apenas após a autenticação bem-sucedida.
A autenticação tradicional com e-mail e senha é a forma de autenticação mais amplamente utilizada e, portanto, amigável. Juntamente com um provedor de identidade confiável, ela oferece segurança equivalente aos sistemas bancários e financeiros tradicionais. Também é possível a autenticação de dois fatores, confirmação por telefone e outras medidas de segurança avançadas.
Resumo
Hoje, estamos dando o primeiro passo na combinação de avanços científicos no campo da criptografia limiar e autenticação tradicional por e-mail. Acreditamos que isso ajudará em nossa missão de promover a adoção do blockchain. Continuaremos nosso trabalho nessa direção. E ainda há muito trabalho a ser feito. Este ano, vamos nos concentrar no desenvolvimento e publicação de materiais, mudando gradualmente para tornar a tecnologia não apenas segura, mas também disponibilizá-la publicamente como código-fonte.
Aqueles que desconfiam dos criptossistemas de limiar ainda podem usar métodos de autenticação tradicionais, com o seed e vários dispositivos, incluindo Ledger.
Em breve, adicionaremos a opção de exportar chaves secretas de contas criadas com e-mail. Mas devemos avisar que este caminho é só de ida. Como resultado desta ação, a conta criada com e-mail será excluída, e o usuário poderá acessar o endereço criado com e-mail, utilizando a chave secreta.
O uso da autenticação por e-mail oferecerá várias outras oportunidades, como:
– alterar a senha
– redefinir a senha
– anexar 2FA, como Google Authenticator
– adicionar recursos extras, incluindo stop loss, take profit etc.
Como trabalhamos constantemente para tornar nosso serviço o mais seguro e fácil de usar, manteremos você informado sobre os desenvolvimentos mais recentes.
Temos o prazer de compartilhar que a tecnologia de autenticação por e-mail já está disponível em dApps de desenvolvedores externos (swop.fi, levex.fi etc.).

